Vector Components
Videos
Used Symbols
counts pos. about |
shows angular pos. of |
relative to |
|
\(\varphi\) |
\(z=\bar z\) |
\((\bar x, \bar y)\) |
\((x, y)\) |
\(\alpha\) |
\(z=\bar z\) |
\(\boldsymbol v'\) |
\(\boldsymbol v\) |
\((x,y)\)-Comp. |
\((\bar x, \bar y)\)-Comp. |
|
\(\boldsymbol v\) |
\(\begin{bmatrix} v_{x}\\ v_{y} \end{bmatrix}\) |
\(\begin{bmatrix} v_{\bar x} \\ v_{\bar y} \end{bmatrix}\) |
\(\boldsymbol v'\) |
\(\begin{bmatrix} v'_{x} \\ v'_{y} \end{bmatrix}\) |
undefined |
Passive und aktive Transformation
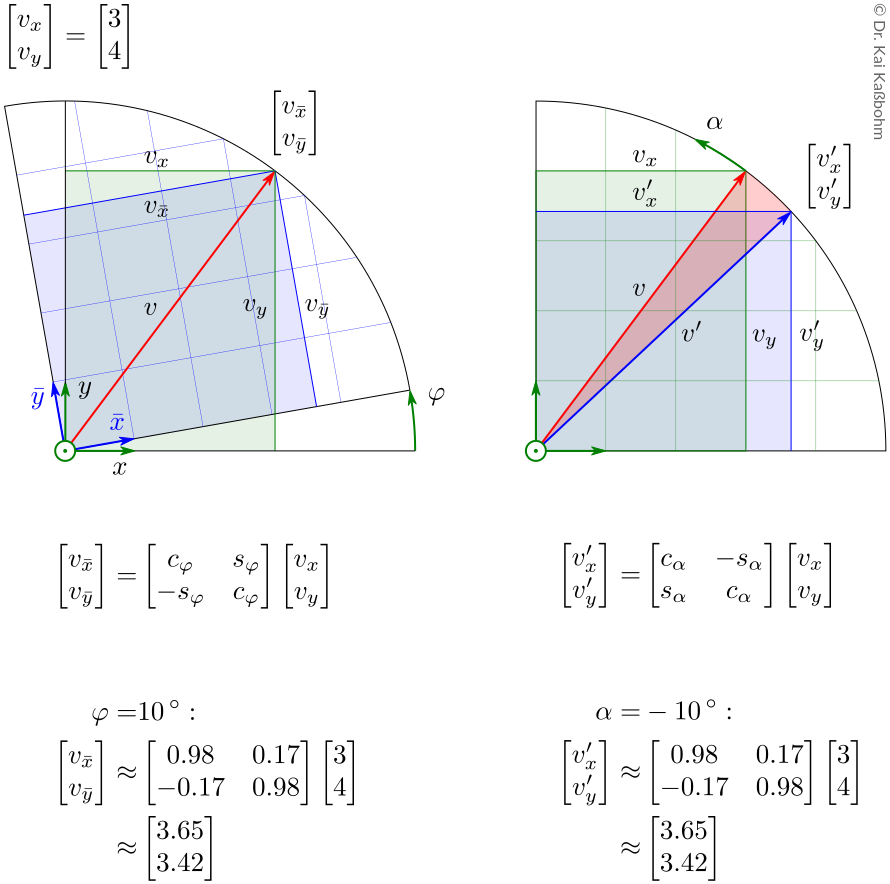
Passive transformation (on the left) und active transformation (on the right) for the special case that \(-\alpha=\varphi\), so that \((v_{\bar x}, v_{\bar y}) = (v'_{x}, v'_{y})\).
Passive und aktive Transformation
For a vector given by its \((x,y)\)-components wrt an \((x,y)\)-frame the following transformations exist:
Passive transformation: 1 Vector & 2 frames: The \((\bar x, \bar y)\)-components of the same vector wrt a second frame is calculated. This second frame is the \((\bar x, \bar y)\)-frame, which is rotated relative to the given \((x, y)\)-frame.
\[\begin{split}\begin{bmatrix} v_{\bar x} \\ v_{\bar y} \end{bmatrix}= \begin{bmatrix} c_\varphi & s_\varphi \\ -s_\varphi & c_\varphi \end{bmatrix} \begin{bmatrix} v_x \\ v_y \end{bmatrix}\end{split}\]Active transformation: 2 Vectors & 1 frame: The \((x, y)\)-components of a second vector are calculated. This second vector is rotated relative to the given vector.
\[\begin{split}\begin{bmatrix} v'_{x} \\ v'_{y} \end{bmatrix} = \begin{bmatrix} c_\alpha & -s_\alpha \\ s_\alpha & c_\alpha \end{bmatrix} \begin{bmatrix} v_x \\ v_y \end{bmatrix}\end{split}\]
Web-App 1
Do a Quiz!
Footnotes:
- 1
Unitless Quantities are used. These are defined as the actual quantity divided by its unit: E.g. if a quantity was given in the unit “meter per second”: The respective unitless quantity would be equal to the given quantity divided by “meter per second”.