Balken-Element B2

• B: Beam, 2: Zwei Knoten

• Beispiele mit Berechnungen siehe hier.

Lineares System

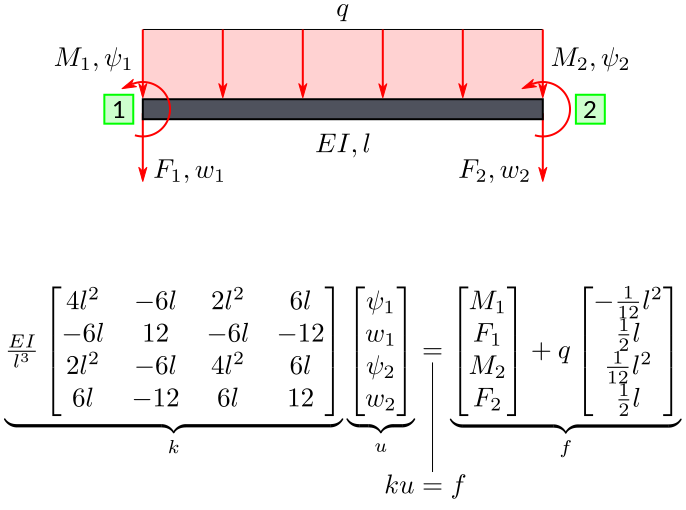
Note

Herleitung dieser Gleichung: B2-der-1 und B2-der-2.

Schreibweisen

Verschiedene Schreibweisen

Es gibt verschiedene Schreibweisen. Denn man kann wählen:

• Welche Symbole man verwendet: \(\psi_1, w_1, \ldots , M_2, F_2\) und \(E, I, l\) können auch anders bezeichnet werden.

• Welche Zählrichtungen man für dievektorwertigen Größen verwendet. D.h. in welche Richtung man die zugehörigen Pfeile zeichnet.

• Wie man die 4 Aussagen in einer Matrix anordnet.

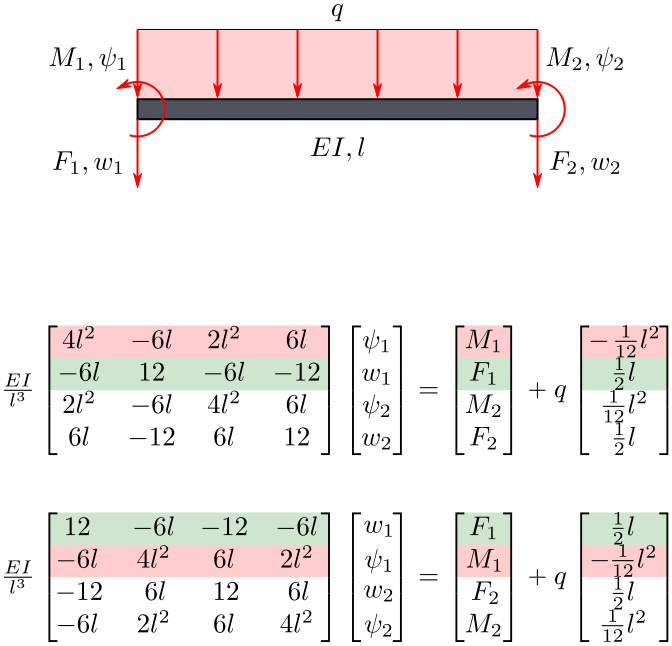
Oben: Hier verwendete Schreibweise. Unten: Schreibweise ähnlich wie im Lehrbuch FEM von Dr. Klein.

Erweiterte Steifigkeitsmatrix

Die erweiterte Element-Steifigkeitsmatrix bietet den Vorteil, dass die Freiheitsgrade \((\psi_1, w_1, \psi_2, w_2)\) sichtbar sind, auf die sich die Einträge der Steifigkeitsmatrix beziehen.

\[\begin{split}k^| = \tfrac{EI}{l^3} \left[ \begin{array}{cccc|c} 4 l^2 & -6 l & 2 l^2 & 6 l & \psi_1 \\ -6 l & 12 & -6 l & -12 & w_1 \\ 2 l^2 & -6 l & 4 l^2 & 6 l & \psi_2 \\ 6 l & -12 & 6 l & 12 & w_2 \\ \end{array} \right]\end{split}\]

Wahl der Knoten-Reihenfolge

Wie beim Stab-Element lässt sich die Knoten-Reihenfolge vertauschen, ohne dass sich die Einträge der Steifigkeitsmatrix ändern:

\begin{align*} \underbrace{ \tfrac{EI}{l^3} \begin{bmatrix} 4 l^2 & -6 l & 2 l^2 & 6 l \\ -6 l & 12 & -6 l & -12 \\ 2 l^2 & -6 l & 4 l^2 & 6 l \\ 6 l & -12 & 6 l & 12 \\ \end{bmatrix} }_k \begin{bmatrix} \psi_1 \\ w_1 \\ \psi_2 \\ w_2 \\ \end{bmatrix} &= \begin{bmatrix} M_1 \\ F_1 \\ M_2 \\ F_2 \\ \end{bmatrix} + q \begin{bmatrix} - \tfrac{1}{12}l^2 \\ \tfrac12 l\\ \tfrac{1}{12}l^2\\ \tfrac12 l \\ \end{bmatrix} \\ \underbrace{ \tfrac{EI}{l^3} \begin{bmatrix} 4 l^2 & -6 l & 2 l^2 & 6 l \\ -6 l & 12 & -6 l & -12 \\ 2 l^2 & -6 l & 4 l^2 & 6 l \\ 6 l & -12 & 6 l & 12 \\ \end{bmatrix} }_k \begin{bmatrix} \psi_2 \\ w_2 \\ \psi_1 \\ w_1 \\ \end{bmatrix} &= \begin{bmatrix} M_2 \\ F_2 \\ M_1 \\ F_1 \\ \end{bmatrix} + q \begin{bmatrix} \tfrac{1}{12}l^2\\ \tfrac12 l \\ - \tfrac{1}{12}l^2 \\ \tfrac12 l\\ \end{bmatrix} \end{align*}

Zugehörige erweiterte Steifigkeitsmatrizen:

\begin{align*} k^| &= \tfrac{EI}{l^3} \left[ \begin{array}{cccc|c} 4 l^2 & -6 l & 2 l^2 & 6 l & \psi_1 \\ -6 l & 12 & -6 l & -12 & w_1 \\ 2 l^2 & -6 l & 4 l^2 & 6 l & \psi_2 \\ 6 l & -12 & 6 l & 12 & w_2 \\ \end{array} \right] \\ k^| &= \tfrac{EI}{l^3} \left[ \begin{array}{cccc|c} 4 l^2 & -6 l & 2 l^2 & 6 l & \psi_2 \\ -6 l & 12 & -6 l & -12 & w_2 \\ 2 l^2 & -6 l & 4 l^2 & 6 l & \psi_1 \\ 6 l & -12 & 6 l & 12 & w_1 \\ \end{array} \right] \end{align*}

Postprocessing / Interpolation

\(N_1, N_2, N_3, N_4, N_5\) sind die dimensionslosen Interpolationsfunktionen:

\[\begin{split}N_1 &= - \xi^{3} + 2 \xi^{2} - \xi\\ N_2 &= 2 \xi^{3} - 3 \xi^{2} + 1 \\ N_3 &= - \xi^{3} + \xi^{2} \\ N_4 &= - 2 \xi^{3} + 3 \xi^{2} \\ N_5 &= \tfrac{\xi^{4}}{24} - \tfrac{\xi^{3}}{12} + \tfrac{\xi^{2}}{24}\\\end{split}\]

Querverschiebung w

Interpolierte Querverschiebung in Matrix-Schreibweise:

\[\begin{split}w &= w_{\psi_1} + w_{w_1} + w_{\psi_2} + w_{w_2} + w_q \\ &= \begin{bmatrix} \psi_1 & w_1 & \psi_2 & w_2 & q \end{bmatrix} \begin{bmatrix} l N_1 \\ N_2 \\ l N_3 \\ N_4 \\ \tfrac{l^4}{B} N_5 \end{bmatrix} \\ &= \begin{bmatrix} \psi_1 & w_1 & \psi_2 & w_2 & q \end{bmatrix} \begin{bmatrix} l \left( - \xi^{3} + 2 \xi^{2} - \xi \right) \\ 2 \xi^{3} - 3 \xi^{2} + 1 \\ l \left( - \xi^{3} + \xi^{2} \right) \\ - 2 \xi^{3} + 3 \xi^{2} \\ \tfrac{l^4}{B} \left( \tfrac{\xi^{4}}{24} - \tfrac{\xi^{3}}{12} + \tfrac{\xi^{2}}{24} \right) \end{bmatrix}\end{split}\]

Note

• Eine \(1 \times 5\)-Matrix multipliziert mit einer \(5 \times 1\)-Matrix ergibt eine \(1 \times 1\)-Matrix, also eine Zahl.

• Man kann das Produkt auch so schreiben:

  \[\begin{split}w &= \underbrace{ \begin{bmatrix} \psi_1 & w_1 & \psi_2 & w_2 & q \end{bmatrix} }_{1 \times 5} \underbrace{ \begin{bmatrix} l N_1 \\ N_2 \\ l N_3 \\ N_4 \\ \tfrac{l^4}{B} N_5 \end{bmatrix} }_{5 \times 1} \\ &= \underbrace{ \begin{bmatrix} l N_1 & N_2 & l N_3 & N_4 & \tfrac{l^4}{B} N_5 \end{bmatrix} }_{1 \times 5} \underbrace{ \begin{bmatrix} \psi_1 \\ w_1 \\ \psi_2 \\ w_2 \\ q \end{bmatrix} }_{5 \times 1}\end{split}\]

• \(w\) ist von der Ordnung \(\xi^4\).

Verdrehung ψ, Biegemoment M, Querkraft Q

Mit \(\psi=-w'\) und \(M = - B w''\) und \(Q = - B w'''\) gilt:

\[\begin{split}\psi &= - \begin{bmatrix} \psi_1 & w_1 & \psi_2 & w_2 & q \end{bmatrix} \begin{bmatrix} l N_1' \\ N_2' \\ l N_3' \\ N_4' \\ \tfrac{l^4}{B} N_5' \end{bmatrix} \\ &= \begin{bmatrix} \psi_1 & w_1 & \psi_2 & w_2 & q \end{bmatrix} \begin{bmatrix} 3 \xi^{2} - 4 \xi + 1\\- \tfrac{1}{l} \left(6 \xi^{2} - 6 \xi\right)\\ 3 \xi^{2} - 2 \xi\\ - \tfrac{1}{l} \left(- 6 \xi^{2} + 6 \xi\right)\\ - \tfrac{l^{3}}{B} \left(\tfrac{\xi^{3}}{6} - \tfrac{\xi^{2}}{4} + \tfrac{\xi}{12}\right) \end{bmatrix}\end{split}\]

---

\[\begin{split}M&= - B \begin{bmatrix} \psi_1 & w_1 & \psi_2 & w_2 & q \end{bmatrix} \begin{bmatrix} l N_1'' \\ N_2'' \\ l N_3'' \\ N_4'' \\ \tfrac{l^4}{B} N_5'' \end{bmatrix} \\ &= \begin{bmatrix} \psi_1 & w_1 & \psi_2 & w_2 & q \end{bmatrix} \begin{bmatrix} - \tfrac{B}{l} \left(- 6 \xi + 4\right) \\ - \tfrac{B}{l^{2}} \left(12 \xi - 6\right) \\ - \tfrac{B}{l} \left(- 6 \xi + 2\right) \\ - \tfrac{B}{l^{2}} \left(- 12 \xi + 6\right) \\ - l^{2} \left(\tfrac{\xi^{2}}{2} - \tfrac{\xi}{2} + \tfrac{1}{12}\right) \end{bmatrix}\end{split}\]

---

\[\begin{split}Q&= - B \begin{bmatrix} \psi_1 & w_1 & \psi_2 & w_2 & q \end{bmatrix} \begin{bmatrix} l N_1''' \\ N_2''' \\ l N_3''' \\ N_4''' \\ \tfrac{l^4}{B} N_5''' \end{bmatrix} \\ &= \begin{bmatrix} \psi_1 & w_1 & \psi_2 & w_2 & q \end{bmatrix} \begin{bmatrix} \tfrac{6 B}{l^{2}}\\ - \tfrac{12 B}{l^{3}}\\ \tfrac{6 B}{l^{2}}\\ \tfrac{12 B}{l^{3}}\\ - l \left(\xi - \tfrac{1}{2}\right) \end{bmatrix}\end{split}\]

Graphische Darstellung

Hinweise zu den Diagrammen

Zwei Interaktive Diagramme

• Schieberegler verschieben = Variieren des Knoten-Werts.

• In Legende Funktion klicken = Aus- und Einblenden des Funktionsgraphen.

• Horizontale Achse: Werte werden nach rechts größer - wie üblich.

• Vertikale Achse: Werte werden nach unten größer.

Querverschiebung, Verdrehung, Biegemoment, Querkraft

Interpolationsfunktionen

Äquivalente Knotenlasten

Video

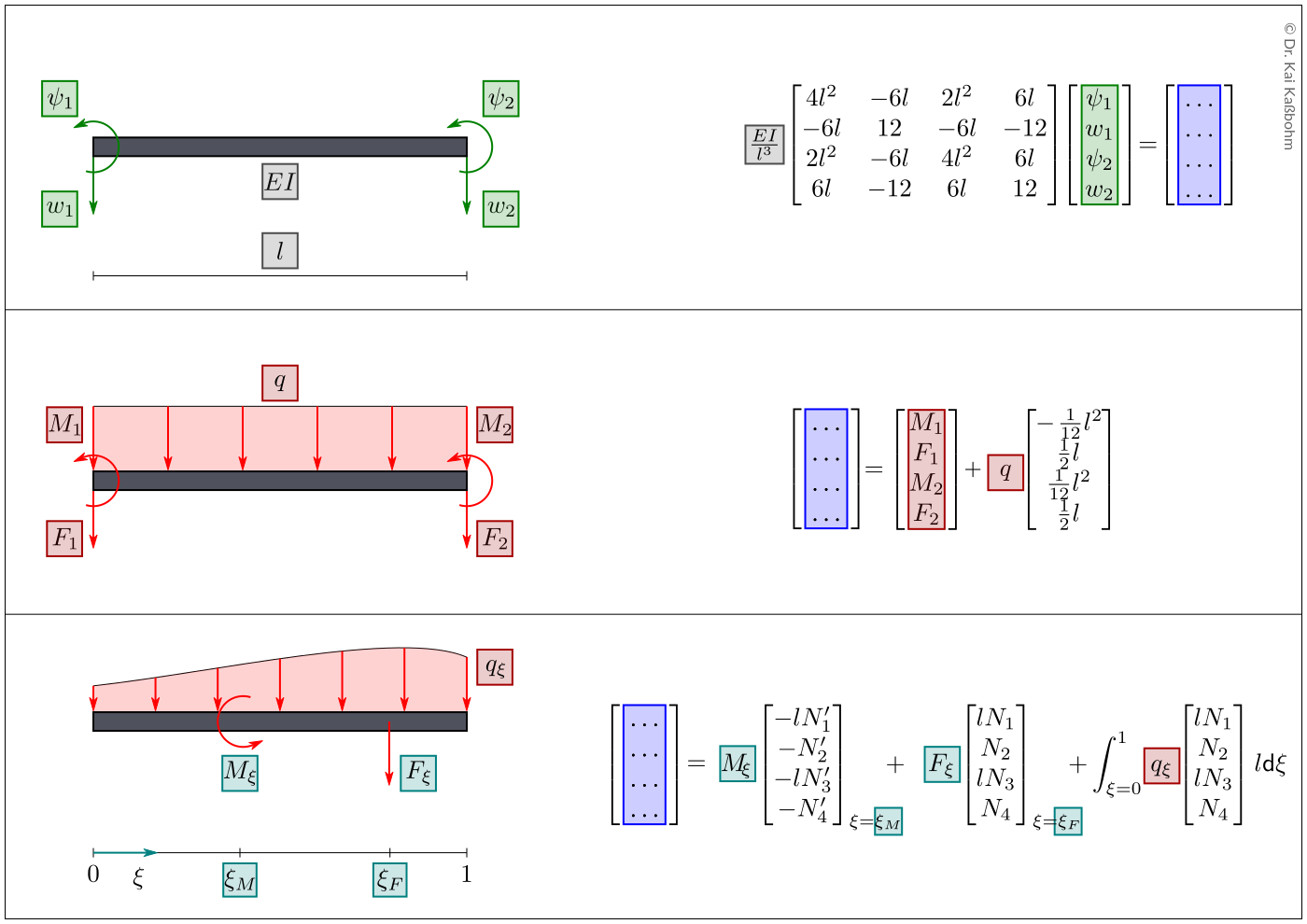
Knotenlasten aufgrund äußerer Lasten \(q_\xi, M_\xi, F_\xi\) zwischen den Element-Knoten. Oben: Lineares System. Mitte: Generische Lasten. Unten: Äquivalente Knotenlasten, Beispiel-Berechnungen hier.

Details

Generische Lasten -> Generische Rechte Seite

• Momente \(M_1, M_2\) sowie Kräfte \(F_1, F_2\) an den Knoten.

• Pro Element konstante verteilte \(q\)-Last.

• Die FEM-Lösung gleicht der klassischen Lösung, denn das Balken-Element wurde definiert, um diese generischen Lasten abzubilden.

• Die rechte Seite \(f\) im Gleichungssystem \(ku = f\) ist:

\[\begin{split}f= \begin{bmatrix} M_1 \\ F_1 \\ M_2 \\ F_2 \\ \end{bmatrix} + q \begin{bmatrix} - \tfrac{1}{12}l^2 \\ \tfrac12 l\\ \tfrac{1}{12}l^2\\ \tfrac12 l \\ \end{bmatrix}\end{split}\]

Sonstige Lasten -> Rechte Seite mit Äquivalenten Knotenlasten

• Momente \(M_\xi\) an beliebiger Position \(\xi_M\) sowie Kräfte \(F_\xi\) an beliebiger Position \(\xi_F\).

• Beliebig verteilte \(q_\xi\)-Last.

• Die FEM-Lösung gleicht nicht der klassischen Lösung.

• Die sonstigen Lasten werden umgerechnet in die Äquivalenten Knotenlasten. 1 Diese Äquivalenten Knotenlasten bilden die rechte Seite \(f\):

\[\begin{split}f = M_\xi \begin{bmatrix} - l N_1' \\ - N_2' \\ - l N_3' \\ - N_4' \\ \end{bmatrix}_{\xi=\xi_M} + F_\xi \begin{bmatrix} l N_1 \\ N_2 \\ l N_3 \\ N_4 \\ \end{bmatrix}_{\xi=\xi_F} + \int_{\xi=0}^1 q_\xi \begin{bmatrix} l N_1 \\ N_2 \\ l N_3 \\ N_4 \\ \end{bmatrix} l \mathsf{d}\xi\end{split}\]

mit Interpolationsfunktionen und deren Ableitungen.

Fußnote:

1

Die bei der Umrechnung verwendete Annahme ist, dass die virtuelle äußere Arbeit der sonstigen Lasten gleich ist der virtuellen äußeren Arbeit der daraus berechneten Äquivalenten Knotenlasten.