3.3.A
Video
Simulation
Two rigid bodies 1 and 2 are connected by a hinge at B.
Particle A on rigid body 1 is moving vertically with velocity \(v_A>0\).
Particle C on rigid body 2 is moving vertically.
Particle D on rigid body 2 is moving horizontally.
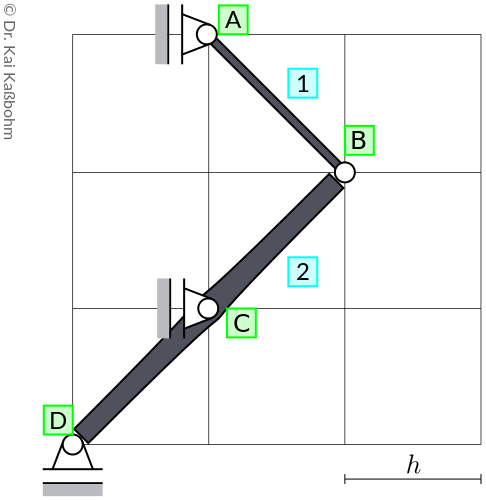
Given symbols: \(h\). Proceed as follows.
Steps
1. Velocities
Use arrows to define:
Velocity \(v_A\) of a particle at A (downward = positive).
Velocity \(v_C\) of a particle at C (downward = positive).
Velocity \(v_D\) of a particle at D (to the left = positive).
Solution
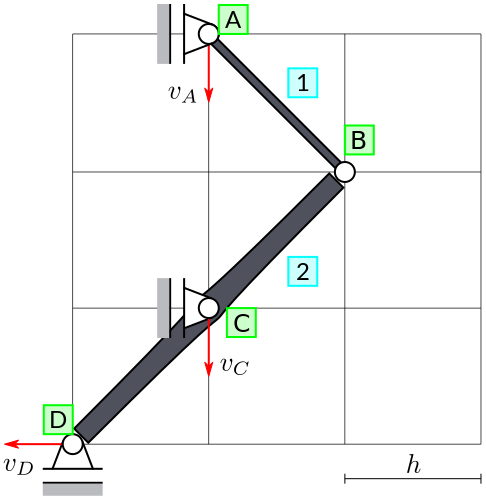
2. Angular Velocity of Body 2
Define the angular velocity \(\omega_2\) of rigid body 2 (clockwise = positive). Draw the respective arrow at the instant centre of rotation of body 2.
Solution
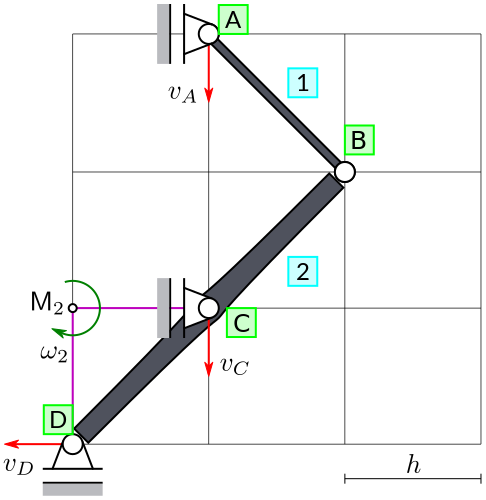
3. Angular Velocity of Body 1
Define the angular velocity \(\omega_1\) of rigid body 1 (counter clockwise = positive). Draw the respective arrow at the instant centre of rotation of body 1.
Solution
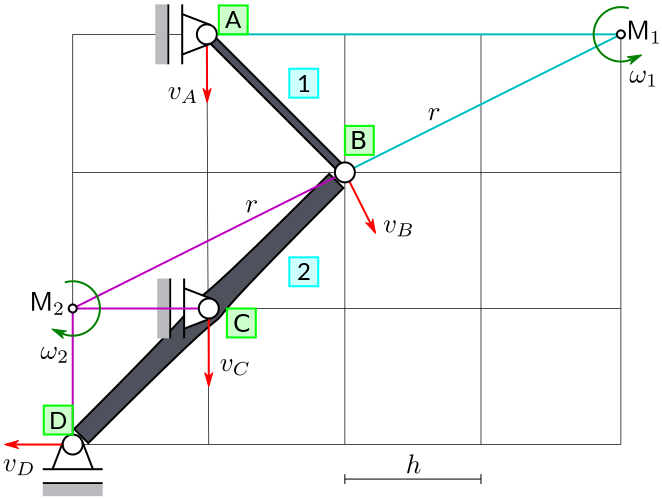
4. Comparing Angular Velocities
Show that:
Solution

So that:
5. Velocity of A
Show that:
Solution

Since \(\omega = \omega_1=\omega_2\):
Therefore:
Find \(v_A\) for the following given quantities:
Solution
6. Angular Velocity of Body 2
Find the angular velocity of body 2 \(\omega_2\) in \(\tfrac{1}{\mathrm s}\) (1 per second) for the same following given quantities:
Solution