Video
Given is a structure consisting of three rods with Young’s Modulus \(E\) und cross-sectional area \(A\).
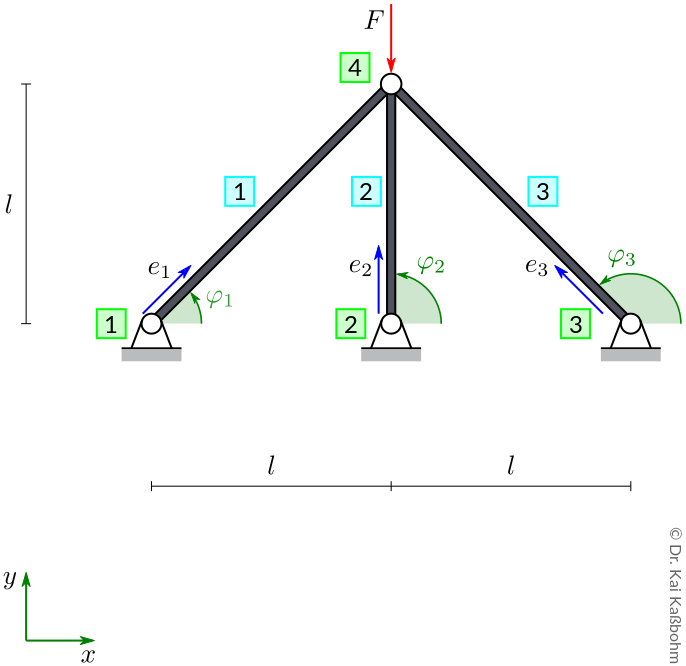
Given symbols: \(F, l, E, A.\)
Use the following shortcuts:
\begin{align*}
\begin{bmatrix}
{\color{green}{c_1}} \\ {\color{green}{s_1}}
\end{bmatrix}
&=
\begin{bmatrix}
\cos \varphi_1 \\ \sin \varphi_1
\end{bmatrix}
=
\begin{bmatrix}
\tfrac{\sqrt 2}{2} \\ \tfrac{\sqrt 2}{2}
\end{bmatrix}
\\
\begin{bmatrix}
{\color{green}{c_2}} \\ {\color{green}{s_2}}
\end{bmatrix}
&=
\begin{bmatrix}
\cos \varphi_2 \\ \sin \varphi_2
\end{bmatrix}
=
\begin{bmatrix}
0 \\ 1
\end{bmatrix}
\\
\begin{bmatrix}
{\color{green}{c_3}} \\ {\color{green}{s_3}}
\end{bmatrix}
&=
\begin{bmatrix}
\cos \varphi_3 \\ \sin \varphi_3
\end{bmatrix}
=
\begin{bmatrix}
-\tfrac{\sqrt 2}{2} \\ \tfrac{\sqrt 2}{2}
\end{bmatrix}
\end{align*}
Proceed as follows:
Steps
1. Equilibrium
Cut around node 1. Note the Equilibrium conditions.
Solution
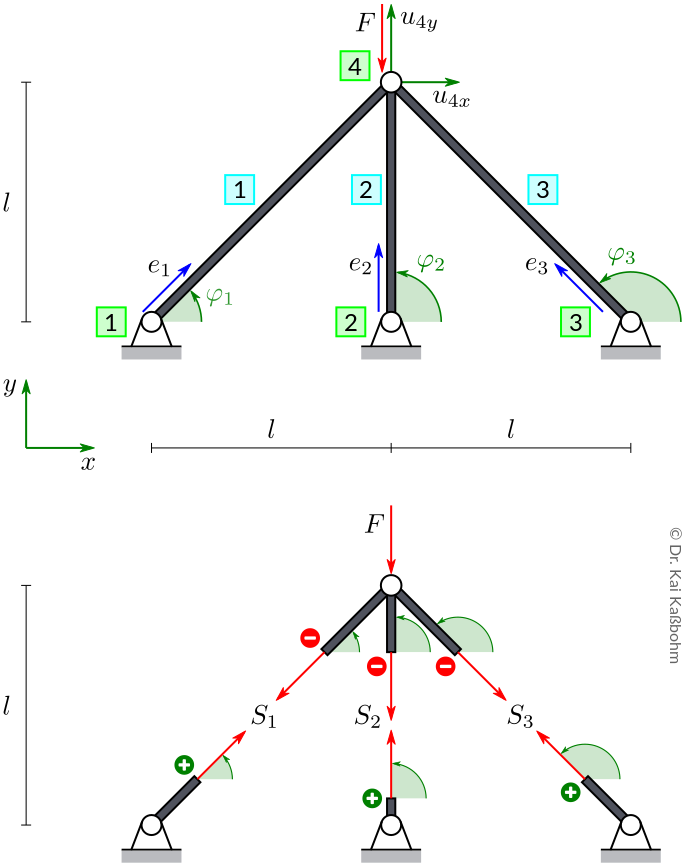
\begin{align}
\rightarrow & & 0 &= - S_1 {\color{green}{c_1}} - S_2 {\color{green}{c_2}} - S_3 {\color{green}{c_3}} \\
\uparrow & & 0 &= - S_1 {\color{green}{s_1}} - S_2 {\color{green}{s_2}} - S_3 {\color{green}{s_3}} - F
\end{align}
Hint
The section force vector on the positive face has the \((x,y)\)-components \((S_1 c_1, S_1 s_1)\).
The section force vector on the negative face has the \((x,y)\)-components \((- S_1 c_1, - S_1 s_1)\).
2. Kinematics: Unit Vectors and Elongations
Find the rod elongations \(\Delta l_1, \Delta l_2, \Delta l_3\) in terms of the \((x,y)\)-components \((u_{4x}, u_{4y})\) of the displacement vector \(\boldsymbol u_4\) of node 4.
Solution
\((x,y)\)-components of the unit vectors:
\begin{align*}
\begin{bmatrix}
e_{1x} \\ e_{1y}
\end{bmatrix}
&=
\begin{bmatrix}
{\color{green}{c_1}} \\ {\color{green}{s_1}}
\end{bmatrix}
\\
\begin{bmatrix}
e_{2x} \\ e_{2y}
\end{bmatrix}
&=
\begin{bmatrix}
{\color{green}{c_2}} \\ {\color{green}{s_2}}
\end{bmatrix}
\\
\begin{bmatrix}
e_{3x} \\ e_{3y}
\end{bmatrix}
&=
\begin{bmatrix}
{\color{green}{c_3}} \\ {\color{green}{s_3}}
\end{bmatrix}
\end{align*}
Elongations:
\begin{align*}
\Delta l_1
&=
\begin{bmatrix}
{\color{green}{c_1}} & {\color{green}{s_1}}
\end{bmatrix}
\begin{bmatrix}
u_{4x} \\ u_{4y}
\end{bmatrix}
\\
&=
\begin{bmatrix}
\tfrac{\sqrt2}{2} & \tfrac{\sqrt2}{2}
\end{bmatrix}
\begin{bmatrix}
u_{4x} \\ u_{4y}
\end{bmatrix} \\
&= \tfrac{\sqrt2}{2} (u_{4x} + u_{4y})\tag{3}
\\
\Delta l_2
&=
\begin{bmatrix}
{\color{green}{c_2}} & {\color{green}{s_2}}
\end{bmatrix}
\begin{bmatrix}
u_{4x} \\ u_{4y}
\end{bmatrix} \\
&=
\begin{bmatrix}
0 & 1
\end{bmatrix}
\begin{bmatrix}
u_{4x} \\ u_{4y}
\end{bmatrix} \\
&= u_{4y}\tag{4}
\\
\Delta l_3
&=
\begin{bmatrix}
{\color{green}{c_3}} & {\color{green}{s_3}}
\end{bmatrix}
\begin{bmatrix}
u_{4x} \\ u_{4y}
\end{bmatrix}
\\
&=
\begin{bmatrix}
\tfrac{-\sqrt2}{2} & \tfrac{\sqrt2}{2}
\end{bmatrix}
\begin{bmatrix}
u_{4x} \\ u_{4y}
\end{bmatrix}
\\
&= \tfrac{\sqrt2}{2} (-u_{4x} + u_{4y})\tag{5}
\end{align*}
3. Elasticity
Find the elongations in terms of the section forces and the given symbols.
Solution
Rod 1 and 3: Length \(\sqrt 2 l\). Rod 2: Length \(l\).
\begin{align}
\Delta l_1 &= \tfrac{S_1}{EA} \sqrt 2 l \tag{6}\\
\Delta l_2 &= \tfrac{S_2}{EA} l \tag{7}\\
\Delta l_3 &= \tfrac{S_3}{EA} \sqrt 2 l \tag{8}
\end{align}
4. System of Equations and Solution
Find in terms of the given symbols:
\begin{align*}
S_1 &= \ldots F \\
S_2 &= \ldots F \\
S_3 &= \ldots F \\
\Delta l_1 &= \ldots \frac{Fl}{EA} \\
\Delta l_2 &= \ldots \frac{Fl}{EA} \\
\Delta l_3 &= \ldots \frac{Fl}{EA} \\
u_{4x} &= \ldots \frac{Fl}{EA} \\
u_{4y} &= \ldots \frac{Fl}{EA}
\end{align*}
For the following quantities:
\begin{align*}
F &= 5\,\mathrm{kN} \\
E &= 200\,\mathrm{GPa} \\
A &= 25\,\mathrm{mm}^2 \\
l &= 1707\,\mathrm{mm}
\end{align*}
Find \(u_{4y}\) in \(\mathrm{mm}\) (millimeters) rounded to \(0.0001\):
\[u_{4y} \approx
\ldots \,
\mathrm{mm}\]
Solution
8 equations to solve for the 8 unknowns \((S_1, S_2, S_3, \Delta l_1, \Delta l_2, \Delta l_3, u_{4x}, u_{4y})\):
\begin{align*}
0 &= S_1 c_1 - S_3 c_1 \tag{1}\\
0 &= F + S_1 c_1 + S_2 + S_3 c_1 \tag{2}\\
\Delta l_1 &= \tfrac{\sqrt2}{2} (u_{4x} + u_{4y}) \tag{3}\\
\Delta l_2 &= u_{4y} \tag{4} \\
\Delta l_3 &= \tfrac{\sqrt2}{2} (-u_{4x} + u_{4y})\tag{5}\\
\Delta l_1 &= \tfrac{S_1}{EA} \sqrt 2 l \tag{6}\\
\Delta l_2 &= \tfrac{S_2}{EA} l \tag{7}\\
\Delta l_3 &= \tfrac{S_3}{EA} \sqrt 2 l\tag{8}
\end{align*}
Solution:
\begin{align*}
S_1 &= \left(-1 + \frac{\sqrt{2}}{2} \right) F \notag \\
S_2 &= \left(-2 + \sqrt{2} \right) F \notag \\
S_3 &= \left(-1 + \frac{\sqrt{2}}{2} \right) F \notag \\
\Delta l_1 &= \left( - \sqrt{2} + 1 \right) \frac{Fl}{EA} \notag \\
\Delta l_2 &= \left( -2 + \sqrt{2} \right) \frac{Fl}{EA} \notag \\
\Delta l_3 &= \left( - \sqrt{2} + 1 \right) \frac{Fl}{EA} \notag \\
u_{4x} &= 0 \cdot \frac{Fl}{EA}\notag \\
u_{4y} &= \left( -2 + \sqrt{2} \right) \frac{Fl}{EA} \notag \\
\notag \\
u_{4y} &\approx-0.9999\,\mathrm{mm}
\end{align*}
5. Symmetry
Show that the same solution can be found by using the symmetry of the system.
Solution
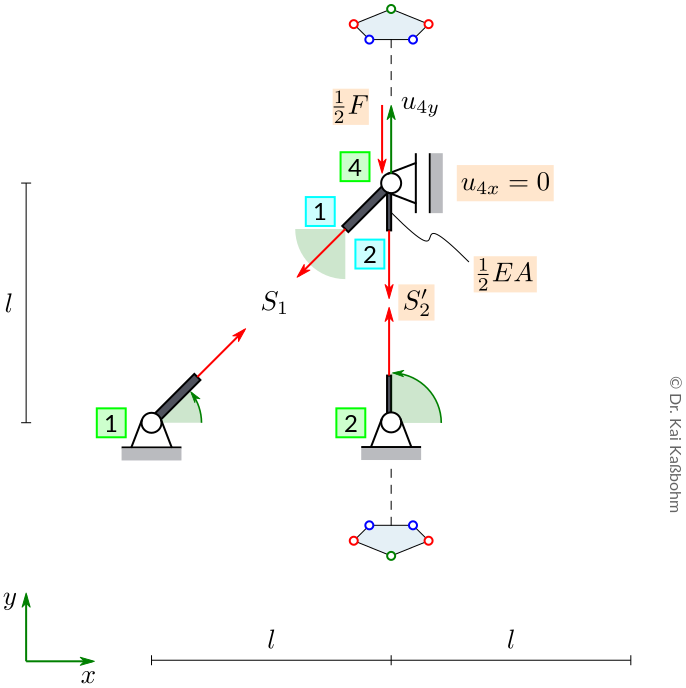
6 equations for the 6 unknowns \((S_1, S_2', \Delta l_1, \Delta l_2, u_{4x}, u_{4y})\):
\begin{align*}
0 &= u_{4x} \tag{1}\\
0 &= \tfrac 1 2 F + S_1 c_1 + S_2' \tag{2} \\
\Delta l_1 &= \tfrac{\sqrt2}{2} (u_{4x} + u_{4y}) \tag{3} \\
\Delta l_2 &= u_{4y} \tag{4} \\
\Delta l_1 &= \tfrac{S_1}{EA} \sqrt 2 l \tag{5} \\
\Delta l_2 &= \tfrac 1 2 \tfrac{S_2}{EA} l \tag{6}
\end{align*}
Solution:
\begin{align*}
S_1 &= \left(-1 + \frac{\sqrt{2}}{2} \right) F \notag \\
S_2' &= \tfrac 1 2 \left(-2 + \sqrt{2} \right) F = \tfrac12 S_2 \notag \\
\Delta l_1 &= \left( - \sqrt{2} + 1 \right) \frac{Fl}{EA} \notag \\
\Delta l_2 &= \left( -2 + \sqrt{2} \right) \frac{Fl}{EA} \notag \\
u_{4x} &= 0 \cdot \frac{Fl}{EA}\notag \\
u_{4y} &= \left( -2 + \sqrt{2} \right) \frac{Fl}{EA} \notag
\end{align*}


